LAwave杨氏模量无损测量系统

应用：薄膜杨氏模量测量

LAwave- 激光噪声方法测试薄膜和材料表面的杨氏模量

LAwave是对薄膜和材料表面进行无损表征的测量系统。它利用短激光脉冲产生表面声波，测量所有频率下波脉冲的传播速度。

所获得的色散曲线取决于表层的弹性模量（杨氏模量）、密度和厚度。

该方法具有广泛的应用领域，包括PVD涂层、CVD涂层、热喷涂涂层、体材料等。此外，可以从弹性行为中获得影响表面和次表面的各种特性，如孔隙度、裂纹、分层、硬化和加工层。

这种测量方法对厚度从几纳米到几百微米不等的粗糙表面的薄膜非常敏感，并可以应用于像聚合物这样的软的材料和像钻石一样硬的材料。

弹性模量是表征材料力学行为的基本材料参数。材料中的原子间键越强，杨氏模量越高。因此，它是一个有用的微观结构指标。微缺陷和孔隙代表材料中缺失的键，这些键会降低杨氏模量，从而可用来评估缺陷密度和孔隙度。

特点：

• 非破坏性
• 薄膜厚度从几纳米到几百微米
• 从聚合物到金刚石的薄膜特性
• 测量时间不到一分钟
• 高重复性
• 测量获得综合特性
• 易于使用
• 配置简单
• 测量面积：最小5×5mm
• 对样本几何尺寸的要求很少
• 表面粗糙度对测量结果影响小

物理原理

表面声波是沿材料表面传播的弹性振动。拉伸在纳米范围内，弹性完全线性，因此，材料不会受到测量的不可逆影响。此外，当波能量集中在表面时，穿透深度仅在波长的尺寸范围内。对于更高的频率，波的穿透深度减小，表面薄膜对表面声波的影响增大。因此，比波长薄得多的薄膜仍然会影响波速。

图1显示了在硅片上测量的色散曲线的两个示例。对于未涂层样品，波速是恒定的，与频率无关。

对于涂有72nm类金刚石碳（DLC）的晶片，由于薄膜的杨氏模量高于衬底，因此速度增加。由于两个样品具有相同的衬底特性，它们的曲线在同一点截距，f=0 MHz时，对应于硅的相速度。

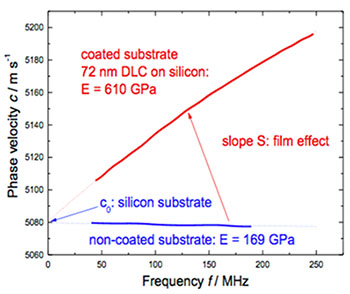
图1：72 nm厚的类金刚石薄膜对应于频率，对声表面波相速度c的影响。实线代表测量数据，虚线代表拟合的理论模型。

在用LAwave系统测量色散曲线后，用数学方法拟合到波传播的理论模型中，在该模型中可以确定相关的材料参数。

技术

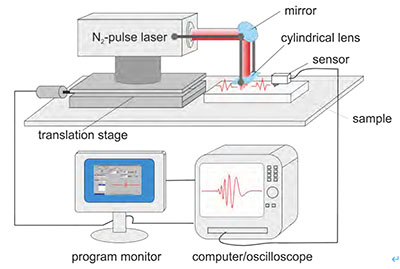
图2: LAwave系统示意图

图2显示了LAwave系统的主要组件。氮脉冲激光器产生表面声波脉冲。这种非接触方法能够准确定位超声源，并可重复产生波脉冲。圆柱透镜将激光束聚焦成一条直线，在该直线上，发射出一道近似的平面波。由于激光脉冲的持续时间较短仅为3纳秒，因此产生了宽频谱的声脉冲。在待测的材料表面传输后，超声波脉冲被与表面接触的声传感器接收到。

传感器的声电特性决定了测量的频率范围。使用频率范围为30 MHz至200 MHz的宽带传感器来测量薄膜。激光声信号由压电PVDF薄膜（聚偏氟乙烯压电薄膜）产生，压电PVDF薄膜通过钢楔连接到样品表面。对于粗糙表面和具有高声阻尼的材料，使用频率范围为2 MHz至20 MHz的超声波标准传感器。

最后，用示波器放大并记录激光声信号。

激光器及其光学元件都固定在平移台上，并一起移动进行一系列测量。这样，激光声信号在离激光聚焦线不同距离的Xi处被检测到。

对信号进行傅里叶变换，得到相位谱i(f) （i=1和2）。色散曲线c（f）可通过以下关系式计算。

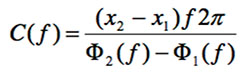
利用两个测量位置之间的测量差异来克服在激光焦点和传感器之间的距离带来的绝对测量的技术困难。

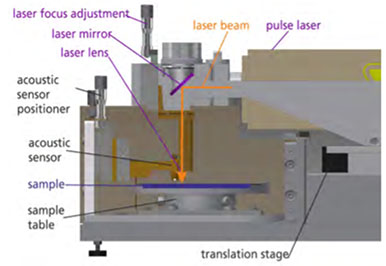
图3:LAwave设备的截面图，显示了激光、光学元件、样品和传感器组件

图3是LAwave设备的示意。它由以下组件组成：

• 将激光束定向到样品表面的反射镜
• 将激光束聚焦在样品表面的柱面透镜
• 调整螺钉，使激光聚焦在样品表面上
• 声传感器
• 手动定位器，用于将传感器连接到样品表面

软件

测量系统包括三个在Windows操作系统上运行的程序。

执行测量的软件如图4和图5所示。它在测量过程中控制激光器、示波器和移动台。在记录了激光焦点线和传感器之间不同距离的一组信号后，计算出色散曲线。图4显示了涂有金刚石膜的硅衬底的示例。

可以保存以下数据：

• ASCII文件中的色散曲线
• 二进制文件中的激光声信号

测量模块的特点是通过将理论曲线拟合到测量曲线上，快速计算薄膜的杨氏模量或厚度。

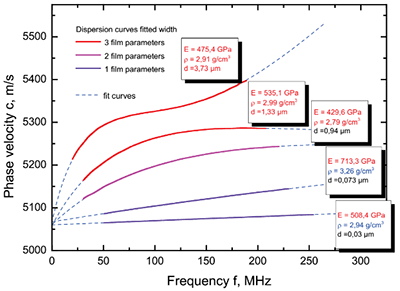
为了进行更详细的分析，提供的曲线拟合软件F5s和F6s，可以拟合多个参数。图6显示了该程序的屏幕截图，其中包括理论中涉及的所有参数：衬底的弹性特性和密度，以及薄膜的弹性特性、密度和厚度。软件F5s支持一层和简单的两层系统，F6s在一个堆栈中最多支持五层测量。

未拟合参数的数据可以手动输入，也可以从数据库中获取，在数据库中可以添加新的材料。

在分析结束时，通过拟合计算出的材料参数可以保存到Excel文件中。

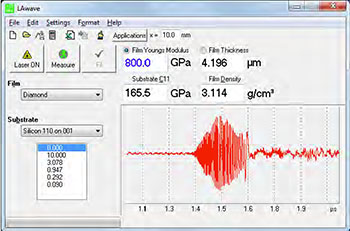
图4：在涂有类金刚石薄膜的硅衬底上检测到的激光声信号

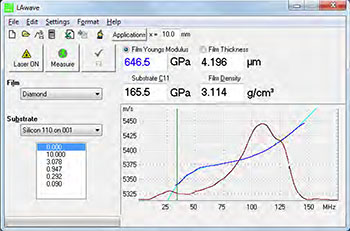
图5: 测量了带有金刚石膜的硅衬底的色散曲线（深蓝色）和拟合的理论色散曲线（浅蓝色）。脉冲幅度显示为棕色线。通过拟合计算了薄膜和衬底的弹性模量。

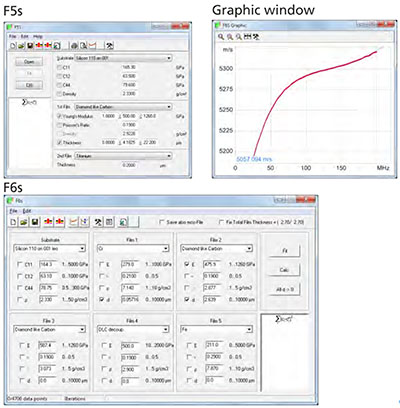
图6：拟合单层（F5s）和多层（F6s）软件系统的程序窗口截图。图形窗口显示了测量的色散曲线和拟合的理论模型。

应用实例

纳米尺寸类金刚石薄膜

• 薄膜厚度：3纳米至100纳米
• 薄膜特性：超硬

对于无氢类金刚石（DLC）薄膜，原子间键的强度决定杨氏模量和硬度。高比例的sp3杂化碳原子将提高整体结合强度，这有利于提高涂层的保护功效。例如，厚度只有几纳米的类金刚石薄膜适合保护计算机硬盘的表面，但可靠地测量此类薄膜的机械性能则比较困难。

在以前的研究中，已经发现无氢类金刚石薄膜的密度和杨氏模量之间存在着经验地关联关系。

这种相关性在材料数据库中有体现，然后在拟合过程中作为附加边界条件考虑进去。

在100 MHz的频率范围内，厚度为几纳米的薄膜每秒只改变几米的波速。因此，在较宽的频率范围内以较高的精度测量速度，这可以通过较长的测量距离实现。

在这种情况下，使用25 mm的距离测量厚度小于10 nm的薄膜。杨氏模量值分散小于5%。由于在本例中研究的是薄膜，计算模量时需要了解薄膜厚度。薄膜厚度可以用椭偏仪测量。

图7显示了厚度为3 nm至约100 nm的类金刚石薄膜的杨氏模量测量值。在10nm以下，随着薄膜厚度的减小，模量逐渐减小。这是由于薄膜表面有一层非常薄的软石墨层，残余应力不足以使碳原子形成类金刚石键。

图7还显示，较低的沉积温度会增加杨氏模量。这一结果表明，随着衬底温度的降低，金刚石键的含量和硬度增加。

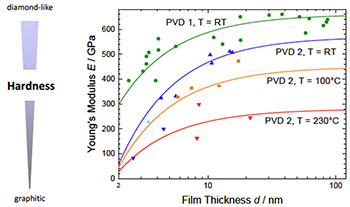
图7：无氢DLC涂层的杨氏模量与涂层厚度的关系，展示了沉积温度和不同PVD技术对杨氏模量的影响。

传感器薄膜

• 薄膜厚度：200纳米至600纳米
• 薄膜性质：聚合物

聚合物薄膜可用于测量湿度、化学物质和机械变形。这种传感器的应用需要了解其机械性能。图8显示了用LAwave法测量的聚酰胺薄膜的杨氏模量和密度与B+离子注入剂量的关系。

利用流变模型，用粘弹性定律描述聚合物的力学性能。与基于准静态变形和样品共振的测试方法相比，LAwave技术可应用于在非常小的变形下有非常高的变形率。因此，该测试得出了聚合物线弹性行为的参数，而粘性流动不受100 MHz范围内频率的刺激。

由于高内耗，高频声波无法穿透聚合物块体。然而，如果聚合物作为足够薄的薄膜沉积在用作声波导的衬底上，则LAwave方法可以进行此类测试。需要考虑的是，薄膜厚度存在一个临界限，超过该临界限，高频表面声波将被聚合物薄膜完全阻尼。根据聚合物材料的性质，该厚度限制在5μm到10μm的范围内。

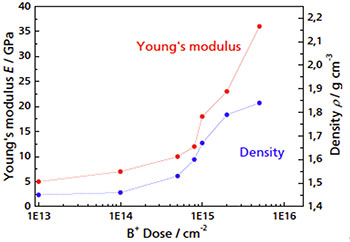
图8：聚合物传感器薄膜的杨氏模量和密度与B+离子注入剂量相比。通过一次测量，拟合色散曲线得出了两个材料参数

衬底损伤

• 损伤深度：高达20μm
• 具有高微缺陷密度的表面

从铸锭上锯切半导体晶片会在表面产生高缺陷密度区域，需要通过仔细的研磨和抛光过程去除该区域。为了优化加工过程，需要确定这种次表面损伤的深度。

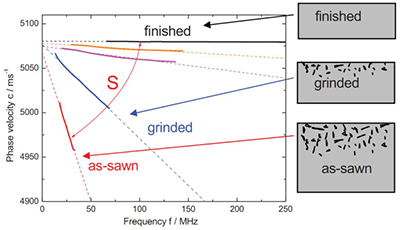
图9显示了在锯切状态下，经过一些研磨步骤后，以及晶圆最终抛光表面的色散曲线。缺陷区具有比基材更低杨氏模量的表面层的效果。因此，色散曲线随着频率的增高而衰减。减薄这一层会降低色散曲线的负斜率。对于成品晶圆，对应于均质材料，测得的色散曲线平行于频率轴。因此，弥散曲线的斜率取决于次表面损伤的深度。

可以建立一个校准函数，根据色散曲线的斜率计算损伤深度。因此，在随后通过蚀刻去除已被确定的损伤层部分的同时，重复测量锯切晶圆。这个过程一直持续到完整的损伤层被移除，等同于体硅材料，色散曲线是一条水平线。

该校准数据库是为该应用提供的LAwave软件版本的一部分。

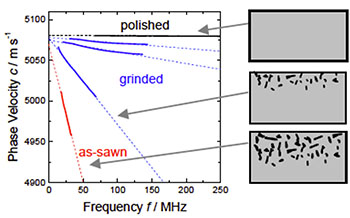
图9：处于锯、磨、抛光状态下，在硅晶片表面测量的色散曲线

热喷涂层

• 涂层厚度：100μm至600μm
• 粗糙的，喷涂表面

热喷涂涂层通常包含制造过程中产生的孔隙。这些气孔可以显著降低涂层的刚度和强度，这使得它们的特性与控制喷涂过程和涂层性能高度相关。传统的表征方法通过制备横截面来进行，既耗时又具有破坏性，大多数零部件无法用此办法。

LAwave方法克服了这些缺点，提供了一种快速、无损的方法来评估热喷涂涂层的孔隙率。

表1比较了测得的喷涂涂层和体材料的杨氏模量。涂层的数值有时远低于体材料的数值，表明涂层中存在大量微孔。结果还表明，涂层质量取决于喷涂技术。HVOF涂层（HVOF-高速氧燃料喷涂）的杨氏模量更高，其次是悬浮喷涂涂层和APS喷涂涂层（APS-大气等离子喷涂）。结果表明，在这种情况下，HVOF涂层更致密，机械强度更高。

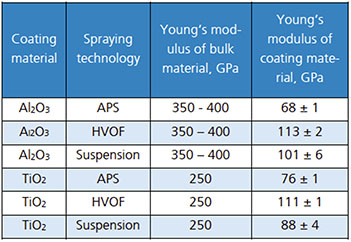
表1：对比于体材料，热喷涂层的杨氏模量

喷涂涂层的粗糙表面往往使测量变得复杂。粗糙度和缺陷也会散射高频超声波。因此，需要在较低的频率下进行测量，这样表面声波能够通过材料。可更换的声学传感器允许选择合适的频率范围。如果是热喷涂涂层，则使用频率范围为2 MHz至20 MHz的传感器。

对应不同热喷涂涂层，研究了粗糙度对激光声学结果的影响，这些涂层分别是喷涂了的表面和喷后研磨以降低粗糙度的表面。

图10两种表面分别对应不同的平均粗糙度指数Ra，将他们的测量结果进行对比。斜率和线性回归的相关系数证实了两个表面的结果有很好的一致性。因此可认为，在几微米范围内的粗糙度不会影响激光声学法的结果。

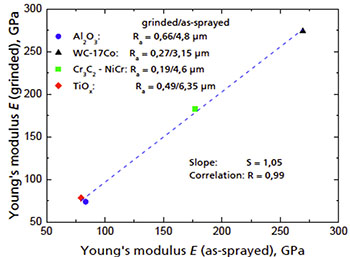
图10：用LAwave测量的不同热喷涂层的杨氏模量对比，对应于粗糙的喷涂表面和研磨表面

LAwave杨氏模量测量系统在硅单晶测量上的应用

背景

目前，半导体产业的主要基础材料依旧是硅单晶材料。作为半导体工业的核心，硅单晶材料如今主要向着两个方向发展：第一、特征线宽不断变小，从而不断提高半导体器件的形核，降低其制造成本；第二，硅片尺寸不断增大，大的硅片尺寸意味着能够在低成本下生产更多的芯片。Gordon Moore在1965年提出了摩尔定律之后，集成电路集成度的发展便几乎契合摩尔定律的规律，从最初的5个晶体管，到目前的超级集成电路可以集成几十亿个元器件。同时硅片尺寸也在不断变大，从4英寸到8英寸，再到后来的12英寸，而今18英寸的硅片的制造技术早已开发完成；FinFET结构在2000年被发明以后，集成电路线宽便得到进一步的缩小。

随着硅单晶尺寸不断变大，硅片本身重力造成的应力和在制造过程中，热处理时硅片体内的热应力都会增大，这会降低后续硅片的光刻精度。硅片在切割、抛光等过程中会受到大于临界切应力的局部应力，这会导致硅片发生接触损伤，这会诱发微裂纹等缺陷，进一步有可能引起硅片的弯曲和破损。因此，硅片的机械性能就成为了影响半导体器件成品率的重要因素。

硅单晶的晶体结构

硅单晶的化学键Si-Si键为共价键，其键强为310KJ mol-1。图1为硅单晶的晶体结构示意图，硅单晶的晶体结构是典型的金刚石立方结构，其晶格常数为0.543nm。硅单晶的最密排面是｛111｝面，密排方向为＜110＞晶向，滑移系为｛111｝＜110＞，因此硅单晶是各向异性材料，同时也是一种脆性材料。

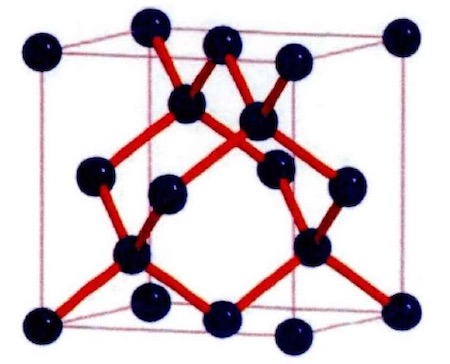
图1 硅单晶结构示意图，球表示硅原子，粗实线表示原子间的成键

杨氏摸量及表面声波

杨氏模量是材料弹性模量的一种，根据胡克定律可以知道模量可以反映材料应力和应变之间的关系。在相同应力条件下，材料发生的应变越大，则材料表现的杨氏模量越低。因此在发生相同的变形时，杨氏模量越高的材料，越容易在载荷卸除后，恢复至加载前的形状。从微观角度上来，当材料被施加载荷时，原子会离开平衡点，就像弹簧被拉伸或是压缩一样，这是杨氏模量越大，原子就越容易回到原来的位置。沸点、熔点、德拜温度等因素会影响原子活动，因此也会影响弹性模量。它们之间存在一定的函数关系。

弹性模量是表征材料力学行为的基本材料参数。材料的原子间键越强，杨氏模量越高。因此，它是一种有用的微观结构指标。微缺陷和气孔代表材料中缺失的键，这降低了杨氏模量，并允许评估缺陷密度和孔隙率。

表面声波是沿材料表面传播的弹性振动。伸长率在纳米范围内，完全线弹性，因此，材料不受测量的不可逆影响。此外，穿透深度仅在波长维度上，波能集中在表面。对于较高的频率，波的穿透深度减小，薄膜对表面声波的影响增大。因此，比波长薄得多的薄膜仍然会影响波速。

LAwave杨氏模量测量系统硅单晶测量应用

（一） 测量单晶材料（例如单晶硅）

由于表面声波的传播速度取决于表面的方向和波在表面上的传播方向，因此可以利用表面声波来分析单晶的方向。

图8.10和8.11显示了没有薄膜的(100)和(111)硅片的结果，结果取决于波的传播方向。对于无涂层晶圆，表面波速度与频率无关。因此，只绘制了一个数据点，代表完整的色散曲线是一条平行于频率轴的直线。

图8.10和8.11表明，表面声波方法揭示了硅晶体的各向异性弹性行为和晶体对称性。

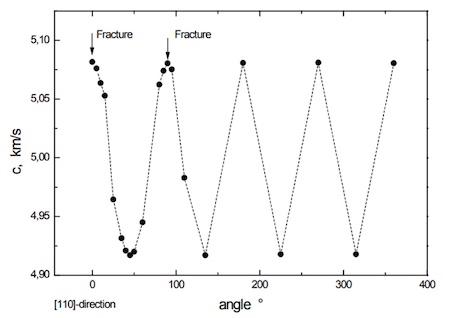
图8.10:(100)硅片表面波速取决于波传播方向，[110]为参考方向。

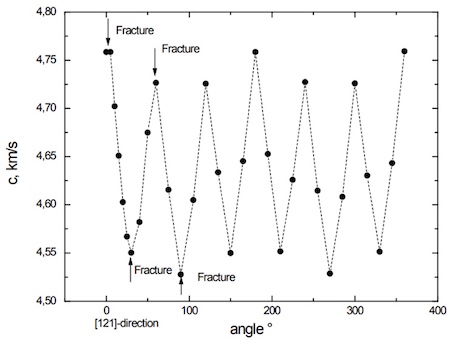
图8.11:(111)硅片表面波速取决于波传播方向;[121]为参考方向。

图8.11表示晶圆切割偏离晶体对称性。这表明这片晶圆没有被切割完全平行于(111)晶体平面。对于正确的方向，图应该是完全周期性的。这表明用表面声波法可以检测晶体的方向。

表面波速在对称方向上的测量对于测试硅或其他单晶材料上的薄膜非常重要。否则不会产生纯表面波(sagital模式)。在(100)平面上，[100]和[110]方向是合适的。[110]方向很容易找到，因为它在晶圆上用一个平面或缺口标记。通常，只有小片的硅片可以作为测试样品。那么，知道(100)晶圆沿[110]方向断裂是有帮助的。测量应该沿着这样的裂缝边缘进行。即使是上升或下降色散曲线，也可以通过外推到零频率来发现晶体的正确方向。在f = 0 MHz时，速度C0表示晶体方向。

注意，要计算薄膜参数，需要选择方向正确的基片材料。测量可在[110]和[100]方向的(100)晶圆上进行。

（二） 测量硅单晶表面的损伤深度

硅单晶的磨削、切割等工艺的设定需要考虑其杨氏模量（将晶棒做成晶片，需要切割磨削等工序）。

亚表面损伤是锯切材料的结果。例如，如果晶圆从硅锭上切割下来，就会发生亚表面损伤。通过研磨或抛光加工表面也会产生损伤层。损伤层深度的确定有助于优化和控制加工过程。

典型的例子是半导体材料上的损伤层。近表面区域的高缺陷密度导致色散曲线随频率下降。损伤层不是均匀的，但在表面有较高的缺陷密度，并逐渐减少到无缺陷的基底。色散曲线的负斜率越陡，损伤越深。然而，当这些值的相关性已知时，可以使用损伤层引起的色散曲线的斜率来计算该损伤层的深度。因此，对于一系列样品，需要用不同的方法(即用LAwave法测量色散曲线的斜率和损伤层的深度，用显微镜在样品的横截面上测量损伤层深度)测量色散曲线的斜率和损伤层深度时，需要采用实验校准程序。图32显示了从铸锭上锯下一个(100)硅片并逐步蚀刻以去除损伤层的色散曲线。去除损伤区域减小了色散曲线的斜率。对于最后抛光阶段，测量一条平行于频率轴的曲线，对应于非涂层硅。

图32:不同刻蚀深度D下(100)硅片[110]方向的硅的色散曲线

结合测量的色散曲线的斜率和蚀刻深度，得到如图33所示的校准曲线。这种相关性在LAwave测量软件中实现。

然而，需要注意的是，该校准仅适用于相同的材料和表面处理。对于硅以外的其他材料，可以导入校准数据。

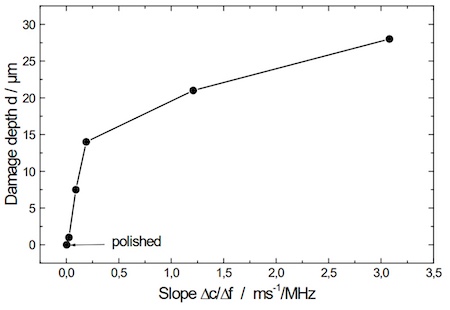
图33:校准表示意图:损伤深度与色散曲线斜率的关系。

损伤层深度的计算方法：

1. 启动校准模式
2. 进入菜单Format
3. 点击校准模式Ctrl+K

程序更改为以下窗口表面:

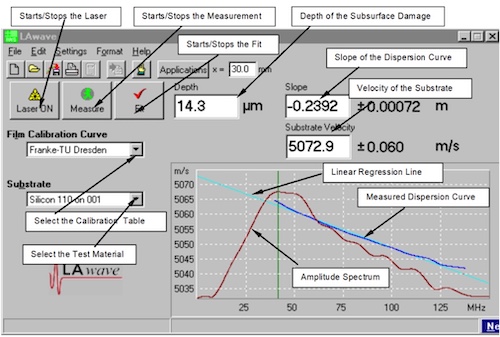
主窗口显示:

• 菜单栏

按钮栏包含以下命令:

• 新建—清除先前的测量值，
• 打开相速度—从硬盘加载色散曲线，
• 保存相速度—保存当前的测量值，
• 打印—打印协议。
• 添加到协议文件-发送拟合的结果(材料参数的值)到协议，文本或Excel文件。
• 应用—选择应用。
• 编辑框x为测量距离。

控制测量的主要命令按钮:

• Laser On—启动激光器。
• Measure—开始测量。
• Fit拟合—启动线性拟合，计算曲线的斜率、基材的相速度C0和损伤深度。

列表框:

• 薄膜校准曲线—从数据库中选择校准表。这个表包含了色散曲线的斜率与基材损伤深度的经验相关性。
• 基材-选择基材材料。

图表

• 测量的色散曲线-深蓝色
• 色散曲线的线性回归线-浅蓝色线
• 测量的振幅谱-棕色线

编辑框:

• 深度-亚表面损伤的深度是最终结果，
• 斜率-由线性回归计算的色散曲线的斜率，
• 基材速度-通过将线性回归线外推到零频率计算出基材的速度C0。

创建损伤深度的校准曲线

• 打开设置菜单。
• 选择材料…
• 点击薄膜校准…

打开以下窗口:

要创建一个新的校准表，请使用“创建数据集”按钮。

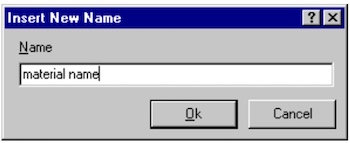
输入校准表的名称。

薄膜校准新/更改窗口打开一个斜率和损伤深度的表。

将校准样品的色散曲线斜率(m/s)/MHz和你测量的损伤深度(μ m)输入到表格中。

注:对于正斜率，损伤深度为负值。为了避免这种情况，在表格的最后一行输入值“1”表示斜率，“0”表示损伤深度。

在表格视图和图形视图之间切换，可以交替查看校准曲线的图表和表格。

如果您想从ascii文件导入校准表，请按“导入文件”按钮。

如果您想将校准表导出到ascii文件中，请按“导出文件”按钮。

（三） 硅基金刚石薄膜

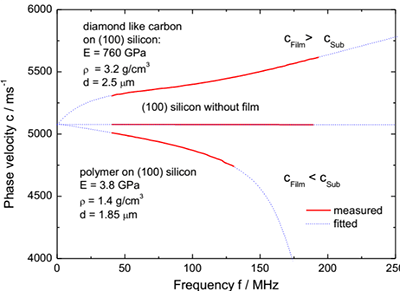
图8.1显示了沉积在(100)硅上的厚度从0.08到5.5微米的金刚石和类金刚石碳薄膜所获得的表面声波色散曲线。给出了实测曲线和拟合曲线。测量方向为[011]。相速度随频率的增加而增加，表明薄膜的相速度高于硅衬底。

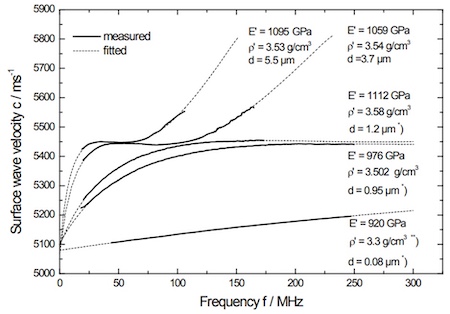
图8.1:沉积在(100)硅上的金刚石和DLC薄膜的表面波速度c与频率f;杨氏模量E′、密度ρ′和薄膜厚度d的拟合结果;
*)厚度d为输入参数;
**)密度ρ′由关系式(8.1)得到

在d = 3.7和5.5 μ m时测量的色散曲线可以拟合三个薄膜参数杨氏模量、密度和薄膜厚度。计算值接近已知的多晶金刚石(E = 1143 GPa， ρ = 3.52 g/cm3)。

对于d = 0.95µm和1.2µm的薄膜，色散曲线的第二次上升移到超出测量带宽的更高频率。与较厚的薄膜相比，信息量减少了。从测量的色散曲线只能得到两个参数。杨氏模量和密度被拟合，因为薄膜厚度可以用触针式仪器得到。

对于特别薄的类金刚石膜(d = 80 nm)，测量了近似线性的色散曲线。它的平稳段超出了测试设备的频率范围。拟合的色散曲线由衬底在零频率下的速度和由薄膜引起的斜率定义。由斜率只能得到一个薄膜参数。引入薄膜厚度和密度，拟合杨氏模量。用椭偏仪测定薄膜厚度。确定薄膜的密度可以通过应用杨氏模量和密度之间的经验关系:

ρ = 1.79 g/cm3 (1 + E/780GPa - (E/1620GPa)2) (8.1)

对于(8.1)关系式，估计∆ρ = ± 0.2 g/ cm3为95%可靠区间。

关系式(8.1)由x射线反射率、卢瑟福背散射和电子能量损失能谱确定薄膜密度的样品系列推导而来。结果如图8.2所示，其中模量随密度单调变化。随着sp3键含量的增加，碳膜变得更加致密和坚硬。

关系式(8.1)已被纳入拟合程序，并允许杨氏模量和密度也被确定适用非常薄的类金刚石碳薄膜。

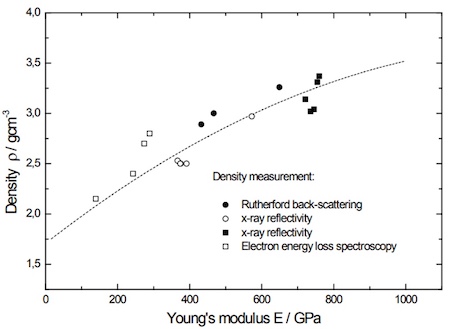
图8.2:非晶态DLC薄膜的密度ρ和杨氏模量E之间的相关性

（四） 硅基超薄类金刚石碳膜的测试

图8.3说明了增加距离X2 - X1对5nm厚度的DLC薄膜(100)硅样品测量误差的影响。它显示了测量的色散曲线是多平滑的，这种非常薄的薄膜的影响越来越多地显示为色散曲线的斜率。色散曲线的不确定度减小为∆c ≤±0.25 m/s对于X2 - X1 = 20 mm。

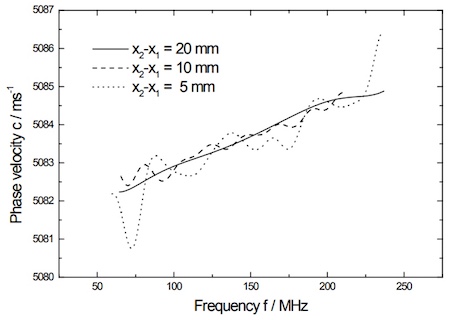
图8.3:测量长度X2 - X1对沉积在(100)硅片上的5nm DLC薄膜测量的色散曲线不确定度的影响

图8.4显示了5nm薄膜与未涂层硅的比较结果。5 nm DLC薄膜的效应在200 MHz带宽内产生3 m/s的斜率。尽管这种小的色散效应，图8.4证明了激光-声学技术能够检测到这种超薄膜。拟合曲线得出的这薄膜杨氏模量为539GPa。

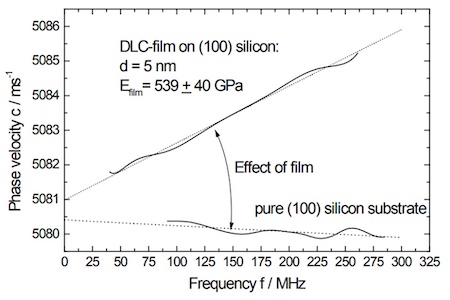
图8.4:在(100)硅上测量厚度为d = 5nm的DLC薄膜和硅片（无薄膜沉积）的色散曲线。给出了拟合的DLC薄膜杨氏模量E

为验证测量不确定度的影响，重复测量10次。薄膜模量分散在∆E ≤±40 Gpa范围内。注意，这种散射远低于测量误差(∆c ≤± 0.25 m/s)与薄膜对色散的影响(在200 MHz带宽内为3 m/s)之比。拟合过程计算理论曲线中所有数据点的平均值。因此，拟合曲线是一条平均曲线，与测量色散曲线中单个点的误差相比，其不确定度较低。

从图8.4中可以看出，即使是纯硅也有少量的表面声波色散。这种大约-0.2 m/s每 200 MHZ的微弱衰减可以解释为衬底材料上的氧化层的影响。涂覆样品的色散曲线被未涂覆硅的曲线的斜率所倾斜，以纠正这种效应。如果没有这个修正，对于5 nm的DLC薄膜，计算的模量仅为502 GPa。尽管氧化层的影响在测量不确定度的量级上，但由于数学拟合的平均效应，可以通过激光-声学方法检测到，如图8.4所示。

（五）硅基氮化硼薄膜

沉积在(100)硅上的120 nm BN薄膜的色散曲线如图8.5[8.1]所示。对沉积工艺进行了优化，以沉积具有优异耐磨性和高温半导体性能的立方氮化硼。已知BN的立方改性具有约680 GPa的高杨氏模量，而六方BN较软，模量仅为35 GPa。这表明需要一种通过测量杨氏模量来表征沉积薄膜材料的方法。测量了不同工艺参数在硅上沉积BN薄膜的色散曲线，如图8.5所示。

图8.5:不同工艺参数沉积在(100)硅上的氮化硼薄膜的色散曲线

曲线的斜率已经表明了薄膜材料的不同质量。一个上升的色散曲线表明，薄膜的杨氏模量与密度之比高于衬底。衰减曲线表明薄膜的这一比率比基片低。图8.5给出了拟合的薄膜模量值。

从图8.6可以看出，这些薄膜的杨氏模量与红外光谱得到的cBN含量相关。在红外光谱中不出现cBN峰时，薄膜模量接近六方BN膜的模量。对于氮化硼薄膜中sp3键比例较高的样品，它会急剧增加。

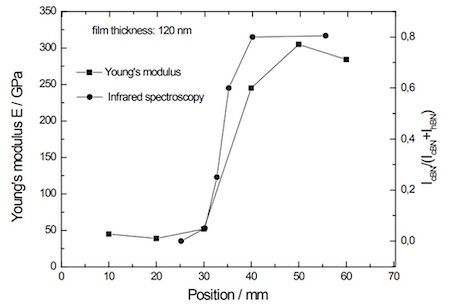
图8.6:红外光谱中杨氏模量与cBN峰强度的相关性

测量知识点：

1、 纳米DLC薄膜

薄膜厚度:3nm ~ 100nm

薄膜性质:超硬

对于无氢类金刚石(DLC)薄膜，原子间键的强度决定了杨氏模量和硬度。高比值的sp3>杂化碳原子会增加整体结合强度，有利于保护涂层的应用。例如，只有几纳米厚度的DLC薄膜适合保护计算机硬盘表面，但很难可靠地测量这种薄膜的机械性能。

在以往的研究中，发现了无氢类金刚石膜的密度与杨氏模量的经验相关性。这种相关性在材料数据库中找到，然后在拟合过程中作为附加的边界条件考虑。

在100兆赫兹的频率范围内，几纳米厚度的薄膜仅以每秒几米的速度改变波速。因此，速度的测量需要在较宽的频率范围内，并具有较高的精度，这可以通过较长的测量距离来实现。

在这种情况下，用25mm的距离来测量厚度小于10nm的薄膜。杨氏模量的离散度小于5%。由于本例中研究的是薄膜，计算杨氏模量时需要薄膜的厚度。用椭偏仪测量薄膜厚度。

2、 聚合物薄膜

聚合物薄膜可用于测量湿度、化学物质和机械变形。应用这种传感器需要了解它们的机械性能。

利用流变学模型，用粘弹性定律描述聚合物的力学性能。与基于准静态变形和样品共振振动的测试方法相比，LAwave技术在非常小的变形下应用了非常高的变形率。因此，测试得到了聚合物线性弹性性能参数，而粘性流动不被100 MHz范围内的频率激发。

由于内部摩擦大，高频声波不能穿透大块聚合物样品。然而，如果聚合物作为足够薄的薄膜沉积在作为声波导的基材（例如硅）上，LAwave方法可以执行这样的测试。需要考虑到有一个膜厚的临界限，超过这个临界限，高频表面声波就会被聚合物膜完全阻尼。根据聚合物材料的性质，该厚度被限制在5 μ m ~ 10 μ m的范围内。

3、 测量准确的色散曲线

随着测量距离的增加和信噪比的提高，色散曲线的精度也随之提高。

影响信噪比的材料性能主要是晶圆表面的粗糙度。它对激光声信号的振幅减小如下:

聚焦的激光能量加热了更大面积的材料表面，伴随着较低的能量密度。这就导致了较低的声波振幅和较低的测量带宽。

建议:激光功率应尽可能高:去除激光束上的滤光片，但避免激光烧蚀损坏表面。

粗糙表面散射声波，声波振幅沿测量距离比光滑表面减小得多。

建议:对于粗糙的表面，使用较短的测量距离，不大于x = 10mm。

粗糙度缩小了测量的带宽，因为加热的表面积更大，声波的散射更能湮灭更高频率的波。这就产生了一个较小的激光声信号，可能会被噪声掩盖，在示波器屏幕上很难看到。

建议:激活20 MHz滤波器:设置菜单-测量…-示波器-带宽限制复选框20 MHz。

对于光滑的晶圆表面，可以测量非常准确的色散曲线，并具有高带宽。这使得测量对非常薄的薄膜很敏感。要做到这一点，不要设置带宽限制，使用一个样本允许的测量距离。